# 一、树结构
# 1、认知
树结构 的应用是非常广泛的,常见的 家族谱、文件目录、公司组织架构等都是树结构。
在我们前端开发中,DOM Tree 更为典型。
# 2、特点
各个方面效率都还可以O(log n):
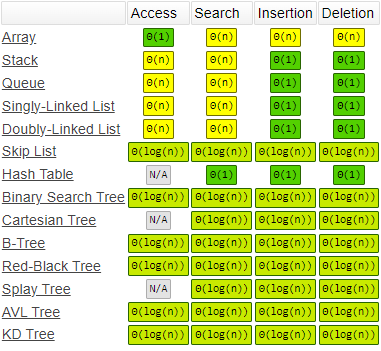
相对于哈希表,树结构空间利用率较高、元素可以是有序的、并且可以快速的找到数组的最值。
# 3、术语
- 树:n(n>=0)个节点构成的有限集合
n = 0 时,我们称为空树
- 节点:
root 根节点、sibling 兄弟节点、leaf node 叶子节点、parent children 父子节点
- 度:
Edge 节点的度、Height 树的度、Level 节点的层次

# 4、表示法
常规表示法

{
element: A,
nextArr: []
}
儿子-兄弟表示法
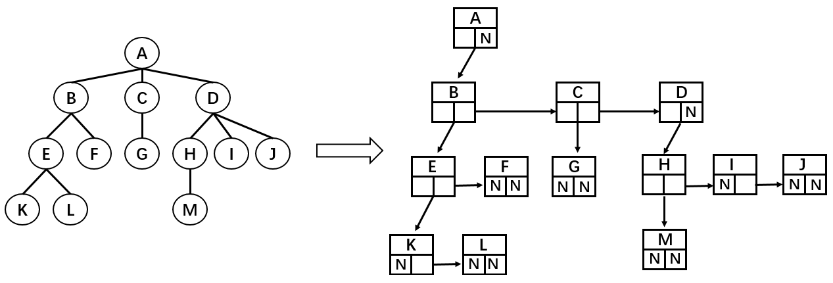
提示:儿子-兄弟表示法 相较于 常规表示法,它巧妙的将所有节点的子节点都固定成了至多两个(也就是下面要讲的 二叉树)
{
element: A,
childNext: BNode
siblingNext: null
}
# 5、分类
具体可以阅读:Useful Tree Data Structures Worth Knowing (opens new window)
- General tree
- Binary tree 二叉树
- Binary search tree 二叉搜索树(BST)
- AVL tree 平衡树(AVL)
- Red-black tree 平衡树(红黑树)
- Splay tree
- Treap
- B-tree
# 二、二叉树
树中的每个节点最多有两个子节点,我们称这要的树为二叉树。
提示
在二叉树中(非空),有一个非常有意思的规律:
left node 叶子节点 = other node 非叶子节点 + 1
# 1、特性
由于二叉树的特性,我们可以知道:
- 第 i 层(Level)最多可以有
2^(i-1)个节点 - 树的度(Height)为 k 时,该树总共最多可以有
2^k - 1个节点 (完美二叉树 Perfect Binary Tree)
# 2、分类
关于二叉树的基础认知,我们可以阅读Tree Data Structures in JavaScript for Beginners (opens new window)
- 满二叉树 Full Binary Tree:每个节点恰好有 0 或 2 个子节点(但绝不是 1)
略
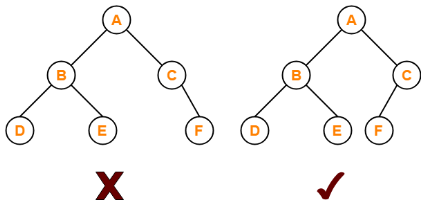
- 完全二叉树 Complete Binary Tree:除最后一层之外的所有层级 Level 都充满节点
堆的本质就是一颗完全二叉树
- 完美二叉树 Perfect Binary Tree:所有级别(包括最后一层)都充满节点时
完美二叉树是一种特殊的完全二叉树

# 3、完全二叉树
按照从上至下,从左到右顺序存储
# 三、BST
# 1、图示
参考:https://en.m.wikipedia.org/wiki/File:Binary_search_tree.svg
例如:在二叉搜索树中添加一个 数据 4

# 2、特点
二叉搜索树是一种特殊的二叉树,它在原二叉树的基础上加了一条限制条件:
左子节点的值 始终小于 右子节点的值
正是因为这个限制条件,在二叉搜索树中,我们可以很快的找到目标数据。
# 3、设计实现
参考:How to Print a Binary Tree (opens new window)、Implementing a Binary Tree in Java (opens new window)
import { ITreeNode } from '../types/INode'
class TreeNode<T> implements ITreeNode<T> {
element: T
left: TreeNode<T> | null = null
right: TreeNode<T> | null = null
constructor(element: T) {
this.element = element
}
}
class BSTree<T> {
private root: TreeNode<T> | null = null
// 供打印树结构使用
get rootNode(): TreeNode<T> | null {
return this.root
}
// -----------------------
// -----------------------
// 递归插入新节点
private insertNode(rootNode: TreeNode<T>, newNode: TreeNode<T>) {
// 判断是否放在 左子树上
if (newNode.element < rootNode.element) {
// 判断左子树上 是否有TreeNode节点
if (rootNode.left !== null) {
this.insertNode(rootNode.left, newNode)
} else {
rootNode.left = newNode // 成功插入TreeNode节点
}
} else {
if (rootNode.right !== null) {
this.insertNode(rootNode.right, newNode)
} else {
rootNode.right = newNode // 成功插入TreeNode节点
}
}
}
// -----------------------
// -----------------------
// 插入新节点
insert(element: T) {
const newNode = new TreeNode(element)
// 是否为空树
if (this.root === null) {
this.root = newNode
} else {
this.insertNode(this.root, newNode)
}
}
}
export default BSTree
# 四、BST 基础操作
# 1、遍历方式
以上面二叉搜索树的示例图为例,不同的遍历结果如下:
- 先序遍历
访问顺序:根节点 --> 左子树 --> 右子树
遍历结果:8、3、1、6、4、7、10、14、13
- 中序遍历
访问顺序:左子树 --> 根节点 --> 右子树
遍历结果:1、3、4、6、7、8、10、13、14
- 后序遍历
访问顺序:左子树 --> 右子树 --> 根节点
遍历结果:1、4、7、6、3、13、14、10、8
- 层序遍历
按照 Level 层次依次访问
# 2、BST 的遍历

- 递归、栈遍历
先序遍历
class BSTree<T> {
// ……
// 先序遍历
preOderTraverse(): T[] {
const resultArr: T[] = []
// 递归也是一个调用栈
function traverseBSTree(rootNode: TreeNode<T> | null) {
if (rootNode) {
resultArr.push(rootNode.element) // 先打印 rootNode 根节点
traverseBSTree(rootNode.left) // 打印 左子树节点
traverseBSTree(rootNode.right) // 打印 右子树节点
}
}
traverseBSTree(this.root)
return resultArr
}
// ……
}
export default BSTree
中序遍历
class BSTree<T> {
// ……
// 中序遍历
inOrderTraverse(): T[] {
const resultArr: T[] = []
// 递归也是一个调用栈
function traverseBSTree(rootNode: TreeNode<T> | null) {
if (rootNode) {
traverseBSTree(rootNode.left) // 打印 左子树节点
resultArr.push(rootNode.element) // 先打印 rootNode 根节点
traverseBSTree(rootNode.right) // 打印 右子树节点
}
}
traverseBSTree(this.root)
return resultArr
}
// ……
}
export default BSTree
后序遍历
class BSTree<T> {
// ……
// 后序遍历
postOrderTraverse(): T[] {
const resultArr: T[] = []
// 递归也是一个调用栈
function traverseBSTree(rootNode: TreeNode<T> | null) {
if (rootNode) {
traverseBSTree(rootNode.left) // 打印 左子树节点
traverseBSTree(rootNode.right) // 打印 右子树节点
resultArr.push(rootNode.element) // 先打印 rootNode 根节点
}
}
traverseBSTree(this.root)
return resultArr
}
// ……
}
export default BSTree
- 队列遍历
层序遍历
class BSTree<T> {
// ……
// 层序遍历
levelOrderTraverse(): T[] {
const resultArr: T[] = []
if (!this.root) return []
// 初始化队列
const queue: TreeNode<T>[] = []
queue.push(this.root) // 入队
// 若有子节点,出队时先将其左右子节点入队
while (queue.length) {
// 记录将要出队的 TreeNode
const temp = queue.shift()!
resultArr.push(temp?.element) // 打印节点
// 将其左右子节点入队
if (temp.left) {
queue.push(temp.left)
}
if (temp.right) {
queue.push(temp.right)
}
}
return resultArr
}
// ……
}
export default BSTree
# 3、BST 的最值
- 最大值、最小值
class BSTree<T> {
// ……
getMaxElement(): T | null {
let temp = this.root
while (temp && temp.right) {
temp = temp.right
}
return temp?.element ?? null
}
getMixElement(): T | null {
let temp = this.root
while (temp && temp.left) {
temp = temp.left
}
return temp?.element ?? null
}
// ……
}
export default BSTree
# 4、BST 搜索节点
- 是否存在某个值
class BSTree<T> {
// ……
getElement(checkElement: T): boolean {
let temp = this.root
while (temp !== null) {
if (temp.element === checkElement) return true
if (temp.element < checkElement) {
temp = temp.right
} else {
temp = temp.left
}
}
return false
}
// ……
}
export default BSTree
# 5、BST 删除节点
对 BST 的节点进行删除操作,大致有下面记住情况:
- 删除的是叶子节点,例如:1、13
- 删除的节点有一个子节点,例如:14、10
- 删除的节点有两个子节点,例如:6、3(难点:删除后的位置填补)
删除 3 时,我们可以采用下面两种节点进行补位:
- 前驱节点(节点 3 的左子树中的最大值) 1 进行补位
- 后继节点(节点 3 的右子树中的最小值) 4 进行补位

class TreeNode<T> implements ITreeNode<T> {
element: T
left: TreeNode<T> | null = null
right: TreeNode<T> | null = null
// 在删除节点时使用
parent: ITreeNode<T> | null = null
get isLeft(): boolean {
return !!(this.parent && this.parent.left === this)
}
get isRight(): boolean {
return !!(this.parent && this.parent.right === this)
}
constructor(element: T) {
this.element = element
}
}
class BSTree<T> {
// ……
// 根据element查找目标节点
private searchNode(checkElement: T): TreeNode<T> | null {
let currentNode = this.root
let parentNode: TreeNode<T> | null = null
while (currentNode !== null) {
if (currentNode.element === checkElement) return currentNode
// 记录当前节点
parentNode = currentNode
// 下移到子节点
if (currentNode.element < checkElement) {
currentNode = currentNode.right
} else {
currentNode = currentNode.left
}
// 追加子节点的parent信息
if (currentNode) currentNode.parent = parentNode
}
return null
}
// 根据目标节点查找其后继节点
private searchSuccessorNode(targetElement: TreeNode<T>): TreeNode<T> | null {
// 后继节点:targetElement的右子树中的最大值
// 右子树
let currentNode = targetElement.right
// 后继节点
let successorNode: TreeNode<T> | null = null
while (currentNode) {
successorNode = currentNode // 左子树节点
currentNode = currentNode.left // 若左子树节点有左子树节点
if (currentNode) {
currentNode.parent = successorNode
}
}
// 数据填充
successorNode!.left = targetElement.left
if (successorNode !== targetElement.right) {
successorNode!.parent!.left = successorNode!.right // 若后继节点有右子节点
successorNode!.right = targetElement.right
}
return successorNode
}
getElement(checkElement: T): boolean {
const isExist = !!this.searchNode(checkElement)
return isExist
}
removeElement(targetElement: T): boolean {
const currentNode = this.searchNode(targetElement)
if (currentNode === null) return false
// 待赋值的treenode节点
let nodeAssignment: TreeNode<T> | null = null
// ---------
// 删除的是叶子节点
if (currentNode.left === null && currentNode.right === null) {
nodeAssignment = null
}
// 删除的节点有一个子节点(左子节点)
else if (currentNode.right === null) {
nodeAssignment = currentNode.left
}
// 删除的节点有一个子节点(右子节点)
else if (currentNode.left === null) {
nodeAssignment = currentNode.right
}
// 删除的节点有两个子节点
else {
const successorNode = this.searchSuccessorNode(currentNode)
nodeAssignment = successorNode
}
// ---------
// 正式执行删除操作
if (currentNode === this.root) this.root = nodeAssignment // 删除的是根节点
if (currentNode.isLeft) currentNode.parent!.left = nodeAssignment
if (currentNode.isRight) currentNode.parent!.right = nodeAssignment
return true
}
// ……
}
export default BSTree
