# 一、图结构
图结构是一种常见的数据结构。比如 webpage 源码设计中的依赖图:

# 1、认知
图是图论(Graph theory)的主要研究对象,它是由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系。
顶点用于代表事物,连接两顶点的边则用于表示两个事物间具有这种关系。
在数学的概念上,树也可以是图的一种。除此之外,与图相关的还有:
- 柯尼斯堡七桥问题
- 最短路问题 👀
- 六度空间理论
- 四色定理
- ……
# 2、特点
图相较于其他数据结构,它的应用范围可以非常广泛,其可以用于建模各种问题。比如:交通网、神经网络等
若往深了研究,它是可以作为一个大的学科的,并且在图的应用方面,还诞生了许多应用广泛的算法。
# 3、术语
- 节点
Vertex 顶点
- 度
Edge 顶点的度
# 4、表示法
对应图来讲,其顶点可以非常方便的表示,但其边的表示方式却又很多不同的方案:
- 领接矩阵
使用 二维数组 来存储 Edge
示意图
注意:如果产生的是一个

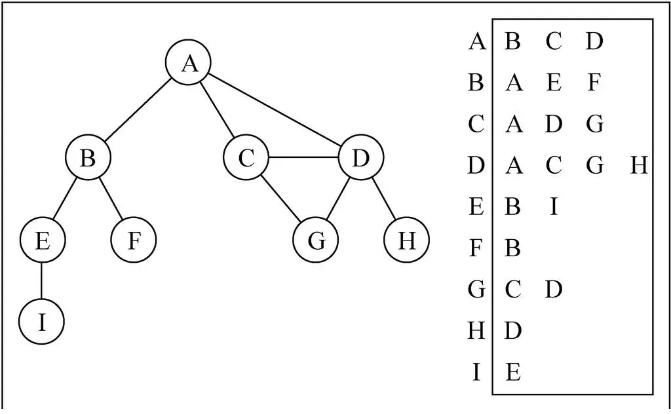
- 领接表 Adjoin List
可以使用 数组/链表/字典(哈希表) 来存储 Edge
示意图
注意:当我们的应用场景是有向图时,为了解决“入度”麻烦的问题,我们可以构造一个“
# 5、分类
有/无向图(方向)、带/无权图(权重)
# 二、无向图
# 1、设计实现
这里采用领接表的方式

class Graph<T> {
private vertexes: T[] = [] // 顶点
private adjList: Map<T, T[]> = new Map() // 领接表
// -----------------------
// -----------------------
// 添加顶点
addVertex(vertex: T) {
this.vertexes.push(vertex)
this.adjList.set(vertex, [])
}
// 添加边
addEdge(v1: T, v2: T) {
this.adjList.get(v1)?.push(v2)
this.adjList.get(v2)?.push(v1)
}
// 查看 图
printGraph() {
this.vertexes.forEach((vertex) => {
const edges = this.adjList.get(vertex)
console.log(`${vertex} -> ${edges?.join(' ')}`)
})
}
}
export default Graph
# 2、遍历方式
与树遍历不同的是,图遍历必须明确指定第一个被访问的 顶点
- 广度优先搜索(Breadth-First Search,简称 BFS)
类似与二叉搜索树中的 层遍历
遍历结果:A、B、C、D、E、F、G、H、I
- 深度优先搜索(Depth-First Search,简称 DFS)
类似与二叉搜索树中的 先序遍历:根节点 --> 左子树 --> 右子树
遍历结果:1、3、4、6、7、8、10、13、14
# 3、BFS 算法
和二叉搜索树中的 层序遍历 一样,我们可以使用队列实现

class Graph<T> {
// ……
// 广度优先搜索
BFSTraverse(): T[] {
const resultArr: T[] = []
if (this.vertexes.length === 0) return []
// 初始化队列
const queue: T[] = []
queue.push(this.vertexes[0]) // 随便指定第一个被访问的 顶点
// 记录已访问的顶点
const visited = new Set()
visited.add(this.vertexes[0])
// 若该顶点有 边,该顶点出队时将其 边对应的顶点入队
while (queue.length) {
const tempVertex = queue.shift()! // 出队
resultArr.push(tempVertex)
// 相邻的顶点
const edgeVertexs = this.adjList.get(tempVertex)
if (edgeVertexs) {
for (const vertex of edgeVertexs) {
if (!visited.has(vertex)) {
visited.add(vertex)
queue.push(vertex)
}
}
} else {
continue
}
}
return resultArr
}
// ……
}
export default Graph
# 4、DFS 算法
在二叉搜索树中的 先序遍历中 使用的是递归,这里我们换一种试试,使用栈实现

class Graph<T> {
// ……
// 深度优先搜索
DFSTraverse() {
const resultArr: T[] = []
if (this.vertexes.length === 0) return []
// 初始化栈
const stack: T[] = []
stack.push(this.vertexes[0]) // 随便指定第一个被访问的 顶点
// 记录已访问的顶点
const visited = new Set()
visited.add(this.vertexes[0])
// 若该顶点有 边,该顶点出栈时将其 边对应的顶点入栈
while (stack.length) {
const tempVertex = stack.pop()! // 出栈
resultArr.push(tempVertex)
// 相邻的顶点
const edgeVertexs = this.adjList.get(tempVertex)
if (edgeVertexs) {
// 反方向入栈(后续就可以正方向出栈了)
for (let i = edgeVertexs.length - 1; i >= 0; i--) {
const vertex = edgeVertexs[i]
if (!visited.has(vertex)) {
visited.add(vertex)
stack.push(vertex)
}
}
} else {
continue
}
}
return resultArr
}
// ……
}
export default Graph
