# 一、堆结构
# 1、认知
堆的本质是一种特殊的树形数据结构,使用完全二叉树来实现。
堆有很多分类,但平时基本使用的都是二叉堆
完全二叉树
按照从上至下,从左到右顺序存储
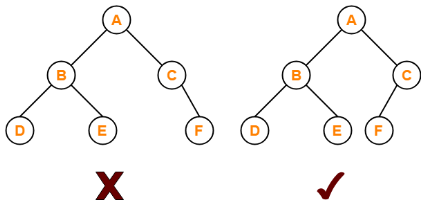
# 2、二叉堆
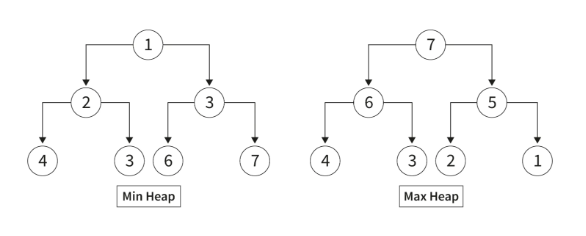
二叉堆还可以划分为:
- 最小堆
- 最大堆
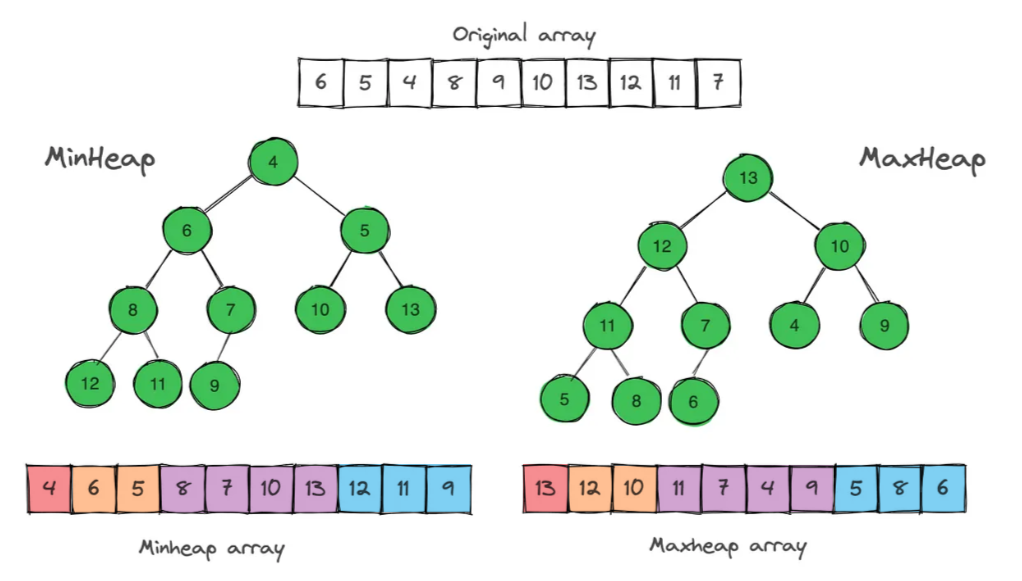
# 3、特点
通常情况下,堆在底层我们会使用数组来实现。并且还有如下规律:
参考:The Generic Way to Implement a Heap in Golang (opens new window)
- 第一个非叶子节点
Math.floor((this.length - 1) / 2) ✖
Math.floor(this.length / 2 - 1) ✔
- 父节点:
floor((i - 1) / 2) - 左子节点:
2i + 1 - 右子节点:
2i + 2
# 4、应用
前面我们使用 BST 进行最值查找时,操作较为复杂,并且还要保证树是平衡的(这样才是 O(logn)级别的)。
而堆可以很好的解决这个问题。
最大堆、最小堆 的 root 元素值就是我们要找的结果
# 二、设计实现
# 说明
下面以设计 最大堆 为例,测试数组为:[100,19,36,17,3,25,1,2,7]
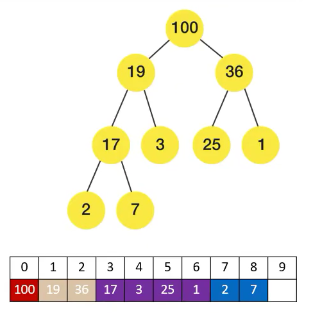
# 1、堆结构设计
class BinaryHeap<T> {
private data: T[] = []
private length: number = 0
// 最大堆、最小堆
private isMaxHeap: boolean = true
constructor(arr: T[] = [], type: 'max' | 'min' = 'max') {
this.isMaxHeap = type === 'max' ? true : false
if (arr.length === 0) return
this.buildHeap(arr)
}
private compareByHeapType(i: number, j: number) {
if (this.isMaxHeap) {
return this.data[i] >= this.data[j]
} else {
return this.data[i] <= this.data[j]
}
}
// 供打印堆结构使用
get heapArr(): T[] {
return this.data
}
// -----------------------
// -----------------------
getMax(): T | undefined {
return this.data[0]
}
get size(): number {
return this.length
}
isEmmpty(): boolean {
return this.length === 0
}
}
# 2、堆操作实现
class BinaryHeap<T> {
// -----
// 根据索引值进行element互换
private swap(i: number, j: number) {
const temp = this.data[i]
this.data[i] = this.data[j]
this.data[j] = temp
}
// 上滤
private heapify_up() {
let elementIndex = this.length - 1
// 上滤到root节点结束
while (elementIndex > 0) {
// 待交换目标
let parentIndex = Math.floor((elementIndex - 1) / 2)
// 判断是否 中途到顶
// if (this.data[parentIndex] >= this.data[elementIndex]) break
if (this.compareByHeapType(parentIndex, elementIndex)) break
// 交换位置
this.swap(elementIndex, parentIndex)
elementIndex = parentIndex // 记录值更新
}
}
// 下滤
private heapify_down(start: number) {
let elementIndex = start
// 没有左子节点结束
while (2 * elementIndex + 1 <= this.length - 1) {
let leftChildIndex = 2 * elementIndex + 1
let rightChildIndex = leftChildIndex + 1
// 待交换目标index(左右子树的较大者)
let largerIndex = leftChildIndex
// if (rightChildIndex < this.length && this.data[rightChildIndex] >= this.data[leftChildIndex]) {
if (
rightChildIndex < this.length &&
this.compareByHeapType(rightChildIndex, leftChildIndex)
) {
largerIndex = rightChildIndex
}
// 判断是否 中途到底
// if (this.data[elementIndex] >= this.data[largerIndex]) break
if (this.compareByHeapType(elementIndex, largerIndex)) break
// 交换位置
this.swap(elementIndex, largerIndex)
elementIndex = largerIndex // 记录值更新
}
}
// -----------------------
// -----------------------
// 原地建堆(自下而上)
buildHeap(arr: T[]) {
this.data = arr
this.length = arr.length
// 最底部的第一个非叶子节点
const start = Math.floor(this.length / 2 - 1)
for (let i = start; i >= 0; i--) {
this.heapify_down(i)
}
}
// 插入元素
insert(element: T) {
// 追加
this.data.push(element)
this.length++
// 上滤
this.heapify_up()
}
// 弹出max元素
extractMax(): T | undefined {
if (this.length === 0) return undefined
if (this.length === 1) {
this.length--
return this.data.shift()
}
// 删除掉max元素
const topElement = this.data[0]
this.data[0] = this.data.pop()!
this.length--
// 下滤
this.heapify_down(0)
return topElement
}
}
← 树结构(Tree) 图结构(Graph) →
