# 一、疑惑解答
# 1、什么是数据结构与算法?
数据结构与算法的本质就是 一门专门研究数据如何组织、存储和操作的科目,但官方并没有明确的定义。
其中,数据操作/使用的效率 与 数据的组织/存储方式紧密相关(比如生活中的快递站)。
Pascal 之父 —— Nicklaus Wirth 曾就凭借:算法 + 数据结构 = 程序(Algorithm + Data Structure = Programs)这一著名公式获得了 图灵奖。
# 2、为什么要学习数据结构与算法?
在常规的开发和学习中,可能我们很少直接接触到 数据结构与算法。但其实它无处不在:
- 常用的前端框架(比如 Vue、React 的源码)中就大量使用了栈结构、队列结构等
- 在 webpack 源码中,也可以看到队列、栈结构、树结构、Graph 图结构
- 还有场景的实现语言或者引擎本身也需要大量的数据结构:哈希表结构、队列结构(微任务队列、宏任务队列)
- 前端开发中更常见的数据结构还有:DOM Tree(树结构)、AST(抽象语法树)
# 3、常见的数据结构有哪些?
提示
其中 数组(Array)、栈(Stack)、队列(Queue)、链表(LinkedList)都属于线性结构。

# 4、常见的算法有哪些?
算法是一组用于执行特定任务或解决特定问题的有序步骤。
它是一种计算过程,可以接受一些输入,经过一系列定义明确的操作,产生输出结果。
Algorithm 这个单词的本意就是解决问题的办法/步骤逻辑,数据结构的实现,离不开算法。
# 二、算法复杂度
# 1、顺序查找
时间复杂度:O(n)
export function sequenceSearch(array: number[], target: number) {
for (let i = 0; i < array.length; i++) {
const item = array[i]
if (item === target) {
return i
}
}
return -1
}
# 2、二分查找
图示:
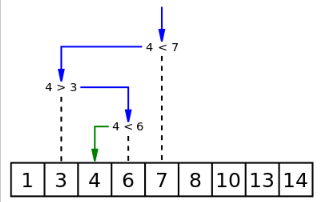
时间复杂度:O(log n)
// 参考:https://simple.wikipedia.org/wiki/Binary_search
export function binarySearch(array: number[], target: number) {
// 索引
let leftIndex = 0
let rightIndex = array.length - 1
while (leftIndex <= rightIndex) {
let midIndex = Math.floor((leftIndex + rightIndex) / 2)
// 中间item
const midItem = array[midIndex]
if (midItem === target) {
return midIndex
} else if (midItem < target) {
leftIndex = midIndex + 1
} else {
rightIndex = midIndex - 1
}
}
return -1
}
# 3、时耗测试
import { sequenceSearch, binarySearch } from '../Search'
// 一个sorted list 排序列表
// const array = [17, 22, 33, 54, 57, 136, 176, 366, 382]
const array = new Array(10000000).fill(0).map((_, index) => index)
const target = 7000000
// 顺序查找
const timeStart = performance.now()
const index_by_sequence = sequenceSearch(array, target)
const timeEnd = performance.now()
console.log(index_by_sequence, '顺序查找-时耗:', timeEnd - timeStart, '毫秒') // 7000000 顺序查找-时耗: 9.334400057792664 毫秒
// 二分查找
const timeOn = performance.now()
const index_by_binary = binarySearch(array, target)
const timeoff = performance.now()
console.log(index_by_binary, '二分查找-时耗:', timeoff - timeOn, '毫秒') // 7000000 二分查找-时耗: 0.1557999849319458 毫秒
# 三、大 O 表示法
参考:https://www.freecodecamp.org/news/big-o-notation-why-it-matters-and-why-it-doesnt-1674cfa8a23c/
# 1、时间复杂度
- O(1):哈希表
- O(log n):Tree 结构(二分查找……)
- O(n):顺序查找
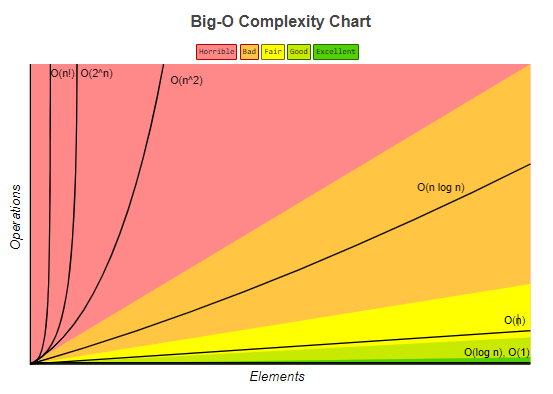
# 2、空间复杂度
空间复杂度很大时,可能会导致内存不足,进而程序奔溃(比如大量递归)
通常不用考虑,有时我们甚至还有 空间换取时间 的需求(比如:动态规划)。
# 3、数据结构对比 🎈
参考:https://www.bigocheatsheet.com/
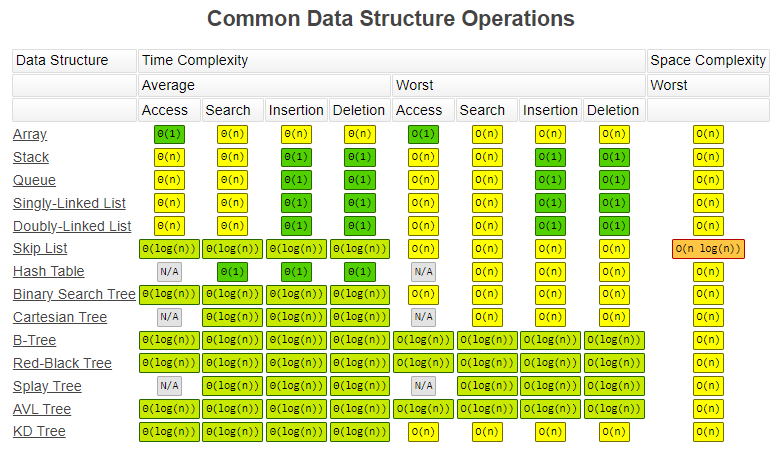
# 4、算法对比
参考:https://www.bigocheatsheet.com/
